
The notion of option-adjusted spread (OAS) was invented about 30 years ago by my colleagues Mike Waldman and Steve Modzelewski in the mortgage research group at Salomon Brothers. Today, OAS is the standard analytical tool for taxable fixed income securities. It is also making inroads into the muni market — better late than never. Unfortunately the usual implementation for munis is flawed, rendering the results virtually meaningless. So it is understandable that many muni professionals shy away from OAS in favor of the archaic 'yield-to-worst' approach. Correct implementation would undoubtedly attract converts.
The Original Objective
Credit spreads relative to a default-free benchmark are of obvious interest to investors. Are they tightening or widening? For taxable bonds, credit spreads relative to Treasuries are available going back to at least the 1960's, and they are published routinely for various categories. Have you ever wondered why similar information is not available for munis?
In the old days, before the introduction of OAS, analysts estimated credit spread by comparing the YTM of the issuer's bond to the YTM of a Treasury bond of like maturity. For the result to be meaningful, both bonds have to be optionless — the yield spread between a 20-year NC-10 corporate bond and a 20-year bullet Treasury would not be informative.
The OAS methodology extends such short-hand estimation of credit spreads to callable bonds by adjusting for the presence of the call option – hence the term 'option-adjusted'. OAS is calculated relative to a risk-free benchmark yield curve, at a specified interest rate volatility, rather than to the YTM of a risk-free bond of matching maturity. It is an estimate of the credit spread at the maturity point corresponding to the expected life of the bond.
As an aside, OAS analysis works perfectly well for optionless bonds, where there is no need to 'option adjust'. Consider, for example, an optionless 4% 20-year corporate bond priced at 107.15 (3.50% YTM). If the 20-year Treasury rate is 2.50%, the OAS turns out to be roughly 100 bps, depending on the shape of the Treasury curve. Because the bond is optionless, the spread could have been calculated on the back of an envelope; the advantage of OAS is that it works for all bonds, callable or not.
What's Wrong with Muni OAS?
The benchmark curves used in the taxable world, namely the Treasury curve and the LIBOR swap curve, are optionless, and therefore need no adjusting. However the standard muni benchmark curves (provided by MMA and MMD, among others) are based on the YTC's of 5% NC-10 bonds. OAS analysis knows how to handle the call option of the bond being analyzed, but it is not smart enough to adjust for the call options in the benchmark curve. An OAS relative to a callable benchmark curve is obviously not a credit spread. So how should it be interpreted? Readers are invited to respond – the Bond Buyer will give a small prize to the best answer.
The Solution
Because a spread relative to a callable benchmark is not a measure of credit risk, the muni world lacks credible historical spread statistics. The solution to estimating meaningful spreads is to convert the benchmark curve into an authentic optionless curve. The method for this is described in "What Makes the Municipal Yield Curve Rise?" (Kalotay-Dorigan).
We note that some vendors provide both callable and optionless benchmark curves. However, they tend to be inconsistent – they cannot be reconciled with each other by rigorous analysis. The basic reason for this is that the callable curves are based on actual market prices, while the optionless curves are educated guesses at best, because long-term optionless muni bonds are virtually non-existent. Therefore we recommend that inconsistencies should be resolved by simply discarding the supplied optionless curve and deriving one from the callable curve.
The attached chart displays a recent 5% NC-10 MMA curve (beyond 10 years) along with the implied optionless par curve, at a 15% volatility. The optionless rates are all considerably higher than the YTC's of the callable bonds of the same maturity; for example the YTC of a 20-year bond is 2.88%, while the implied optionless 20-year par rate is 3.46%. Thus an OAS relative to an optionless curve will be significantly smaller.
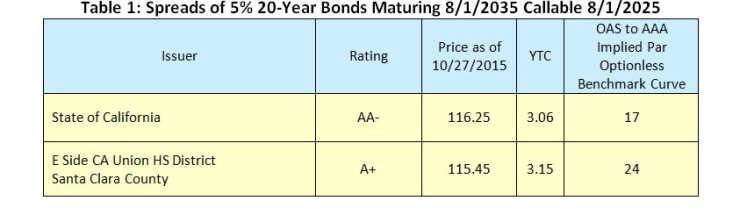
Let's consider two real 5% bonds maturing on August 1, 2035 and callable on August 1, 2025; one rated AA- and the other A+, shown in the attached table. Based on their prices as of October 27, 2015, we observe that the OAS's calculated relative to the implied optionless par yield curve produce reasonable results — 17bps for the AA- bond and 24bps for the A+ bond.
Let's keep in mind that these results depend on the assumed interest rate volatility, here 15%. Increasing the volatility would also increase the OAS. Another relevant parameter is the mean reversion factor, here 0 – a positive mean reversion factor would reduce the OAS. A discussion on the choice of these parameters is beyond the scope of this article.
In any spread analysis of munis, not limited to OAS, there is another hurdle that needs to be overcome: the market price of a muni selling at a discount incorporates the tax to be paid by the buyer at maturity. This tax payment, which is unrelated to credit, nevertheless depresses the price. Any analysis that does not adjust for tax effects is certain to overestimate the credit spread of a discount muni, possibly by a wide margin. The correct approach is to use the so-called tax-neutral valuation.
In summary, two critical fixes are needed to make OAS for munis meaningful as credit spreads. First, use an optionless benchmark curve. For internal consistency, the implied optionless curve extracted from a 5% NC-10 benchmark curve is recommended. Second, tax-neutral valuation is needed to properly account for the tax effect that depresses discount prices.





